Только самые мудрые и самые глупые не поддаются обучению. Конфуций

Задание № 4 (в 2020 году это было задание № 5)

Спецификация контрольных измерительных материалов единого государственного экзамена по информатике и ИКТ

Проверяемые элементы содержания	Уровень сложности задания	Макс. балл за выполнение задания	Примерное время выполнения задания (мин.)
Умение кодировать и декодировать информацию	Базовый	1	2

 

---

Практика

Разберем примеры заданий из ЕГЭ прошлых лет

1. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Вот этот код:

А – 00, Б – 01, В – 100, Г – 101, Д – 110. Можно ли сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно? Коды остальных букв меняться не должны. Выберите правильный вариант ответа.
1) для буквы Д – 11
2) это невозможно
3) для буквы Г – 10
4) для буквы Д – 10

При решении этого задания можно попробовать подобрать такую цепочку из кодов букв, которая бы однозначно была декодирована или, наоборот, не однозначно была бы декодирована, и проанализировать варианты. Но можно быстрее решить это задание, воспользовавшись условием Фано (смотри в теории). Проверим, можно ли сократить код буквы Г до 10. В этом случае нарушается условие Фано, т.е. код буквы Г станет началом кода буквы В, однозначное декодирование невозможно. То же самое мы видим, если сократим код буквы Д до 10. Не подходит и этот вариант. А если код буквы Д сократить до 11, то этот код не является ни началом, ни концом какого-либо кода. Это и есть ответ.

Ответ: 1

2. Для передачи данных по каналу связи используется 5-битовый код. Сообщение содержит только буквы А, Б и В, которые кодируются следующими кодовыми словами:

A – 11010, Б – 00110, В – 10101.
При передаче возможны помехи. Однако некоторые ошибки можно попытаться исправить. Любые два из этих трёх кодовых слов отличаются друг от друга не менее чем в трёх позициях. Поэтому если при передаче слова произошла ошибка не более чем в одной позиции, то можно сделать обоснованное предположение о том, какая буква передавалась. (Говорят, что «код исправляет одну ошибку».) Например, если получено кодовое слово 10110, считается, что передавалась буква Б. (Отличие от кодового слова для Б – только в одной позиции, для остальных кодовых слов отличий больше.)
Если принятое кодовое слово отличается от кодовых слов для букв А, Б, В более чем в одной позиции, то считается, что произошла ошибка (она обозначается ‘x’).
Получено сообщение 00111 11110 11000 10111. Декодируйте это сообщение – выберите правильный вариант.
1) БААВ
2) БААx
3) xxxx
4) xААx

Я расположу коды букв столбиком под каждое из полученных кодовых слов:

	00111	11110	11000	10111
А	11010	11010	11010	11010
Б	00110	00110	00110	00110
В	10101	10101	10101	10101

 Я выделила красным цветом те цифры, которые отличаются в кодах слов, причем у тех букв, где не более одного отличия. Таким образом, полученное сообщение можно декодировать как БААВ.

 Ответ: 1

 

 

 

3. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Вот этот код:

А – 0; Б – 100; В – 1010; Г – 111; Д – 110. Требуется сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно. Коды остальных букв меняться не должны.
Каким из указанных способов это можно сделать?
1) для буквы В – 101
2) это невозможно
3) для буквы В – 010
4) для буквы Б – 10

Это задание практически не отличается от первого, попробуйте решить его самостоятельно.

4. Для кодирования некоторой последовательности, состоящей из букв Л,М, Н, П, Р, решили использовать неравномерный двоичный код,
удовлетворяющий условию, что никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Для букв Л, М, Н использовали соответственно кодовые слова 00, 01, 11. Для двух оставшихся букв – П и Р – кодовые слова неизвестны.
Укажите кратчайшее возможное кодовое слово для буквы П, при котором код будет удовлетворять указанному условию. Если таких кодов несколько, укажите код с наименьшим числовым значением.

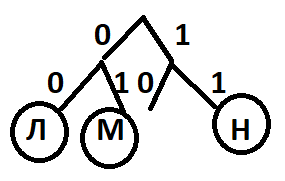Начертим двоичное дерево (смотри рисунок слева) и укажем на нем уже известные коды букв Л, М и Н. У нас есть один свободный "хвост", на который хотелось бы разместить букву П, таким образом получим кратчайший код. Но так делать НЕЛЬЗЯ, потому что есть еще одна буква, для которой должен быть свой код, так как в задании написано, что последовательность состоит из букв Л, М, Н, П, Р.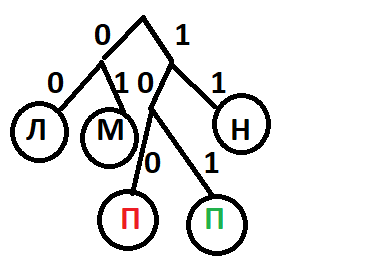 

Значит нам необходимо продлить ветки дерева (смотри рисунок справа).

Теперь мы можем составить код для буквы П двумя способами - это 100 (обозначено красным цветом) и 101 (обозначено зеленым цветом). Среди этих двух нужно выбрать код с наименьшим числовым значением, а это 100.

Ответ: 100

 

И, в заключение, рекомендую пройти онлайн-тест В5 на сайте К.Полякова (выбрать)