Правильный путь такой: усвой то, что сделали твои предшественники и иди дальше
Л. Толстой

Задание № 11

Спецификация контрольных измерительных материалов единого государственного экзамена по информатике и ИКТ

Проверяемые элементы содержания	Уровень сложности задания	Макс. балл за выполнение задания	Примерное время выполнения задания (мин.)
Умение исполнить рекурсивный алгоритм	Базовый	1	5

Теория

Используя следующие материалы, можно повторить необходимые теоретические вопросы.

Материалы с сайта Фоксфорд:

Процедуры и функции в Pascal (смотреть)

Практика

Разберем примеры заданий из ЕГЭ прошлых лет

1. Ниже записан рекурсивный алгоритм F.

procedure F(n: integer);
begin
writeln(n);
if n < 5 then
begin
F(n + 1);
F(n + 3)
end
end
Чему равна сумма всех чисел, напечатанных на экране при выполнении вызова F(1)

Решение:

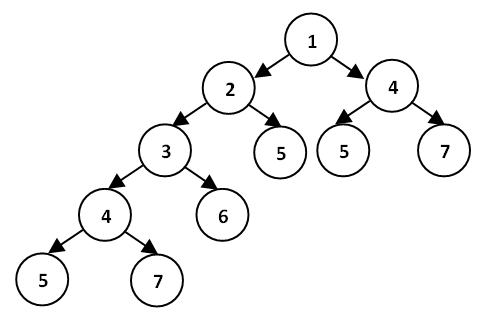Т.к. в данном задании в самой процедуре дважды вызывается рекурсивно сама же процедура, то нагляднее всего построить дерево решения задачи, вершинами которого будут текущие значения n, и, соответственно, эти числа и будут напечатаны.

Рисование дерева ограничивается условием n<5, как только это условие не выполняется, прекращается вызов процедур. Осталось только сосчитать сумму всех цифр.

Ответ: 49

2. Ниже записаны две рекурсивные функции (процедуры): F и G.

procedure F(n: integer); forward;
procedure G(n: integer); forward;

procedure F(n: integer);
begin
if n > 0 then
G(n - 1);
end;
procedure G(n: integer);
begin
writeln('*');
if n > 1 then
F(n - 3);
end;

Сколько символов «звёздочка» будет напечатано на экране при выполнении вызова F(11)?

Решение: В этом задании присутствуют две процедуры, взаимно вызывающие друг друга, причем "звездочка" печатается только при вызове процедуры G. Здесь также есть ограничения: вызов процедуры G прекращается при невыполнении условия n>0, а вызов процедуры F прекращается при невыполнении условия n>1. Оформим решение в виде таблицы, сначала осуществляется вызов F(11), поэтому вначале поместим это значение.

вызываемая функция	F(11)	G(10)	F(7)	G(6)	F(3)	G(2)	F(-1)
проверяемое условие	11>0	10>1	7>0	6>1	3>0	2>1	-1>0

Количество напечатанных "звездочек" будет равно количеству вызываемой процедуры G.

Ответ: 3