Ученик никогда не превзойдет учителя, если видит в нем образец, а не соперника.. Виссарион Григорьевич Белинский

Задание № 14 (в 2020 году это было задание № 16)

Спецификация контрольных измерительных материалов единого государственного экзамена по информатике и ИКТ

Проверяемые элементы содержания	Уровень сложности задания	Макс. балл за выполнение задания	Примерное время выполнения задания (мин.)
Знание позиционных  систем  счисления	Повышенный	1	5

---

Теория

Используя данные материалы, можно повторить необходимые теоретические вопросы.

• Материалы единой коллекции ЦОР (цифровых образовательных ресурсов):​
  • Развернутая форма записи числа
  • Перевод недесятичных чисел в десятичную систему счисления
  • Преобразование десятичного числа в другую систему счисления
  • Преобразование чисел между системами счисления 2, 8, 16
  • Сложение и вычитание одноразрядных двоичных чисел
  • Сложение и вычитание многоразрядных двоичных чисел
  • Умножение и деление двоичных чисел

---

Практика

Разберем примеры заданий из ЕГЭ прошлых лет

1. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 39 оканчивается на 3.

При делении числа 39 на основание системы счисления, в которую переводим, первый остаток должен быть равен 3 (т.к. именно он будет находиться в конце записи числа). Самым большим основанием является 36. А остальные основания будут являться делителями числа 36, т.е. 18, 12, 9, 6, 4, 3, 2.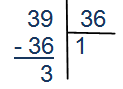 

Не забудьте записывать ответ в правильном порядке.

Ответ: 2,3,4,6,12,18,36

2. В системе счисления с некоторым основанием десятичное число 129 записывается как 1004. Укажите это основание.

Решать данную задачу можно подбором, деля число 129 на различные основания. Уменьшить количество вариантов можно следующими рассуждениями: т.к. новая запись числа (1004) стала длиннее, значит основание системы меньше 10. Число 1004 оканчивается на 4, значит, первый остаток при делении будет равен 4.

Другой способ предполагает решение следующего уравнения:

1*x³ + 0*x² + 0*x¹ + 4*x⁰ = 129, здесь число 1004_х записано в развернутой форме.

3. Укажите наименьшее основание системы счисления, в которой запись десятичного числа 30 имеет ровно три значащих разряда.

​Решать данную задачу также можно подбором, деля число 30 на различные основания. При этом нужно обратить внимание на то, что новая система счисления должна иметь основание не большее 10, т.к. новая запись числа будет длиннее, чем десятичная.

4. Запись десятичного числа в системах счисления с основаниями 3 и 5 в обоих случаях имеет последней цифрой 0. Какое минимальное натуральное десятичное число удовлетворяет этому требованию?

Т.к. запись десятичного числа в системах счисления с основаниями 3 и 5 в обоих случаях имеет последней цифрой 0, значит, что десятичное число кратно 3 и 5 (первый остаток от деления равен 0). Минимальное натуральное десятичное число, кратное 3 и 5 - это 15. Действительно, 15₁₀ = 120₃ = 30₅.​

Ответ: 15 

5. Сколько единиц содержится в двоичной записи значения выражения: 4²⁰¹⁴ + 2²⁰¹⁵ - 8

В первую очередь необходимо представить все числа в виде степеней числа 2:  2⁴⁰²⁸ + 2²⁰¹⁵ -2³ (вспомним математику). Вспомним, что 2⁰ = 1₁₀ = 1₂, 2¹ = 2₁₀ = 10₂, 2² = 4₁₀ = 100₂, и т.д. Мы видим, что в числе 2ⁿ одна единица и n нулей, значит при сложении двух чисел, представляющих степени числа 2 (но только у которых степени не равны), получится две единицы, а нулей, соответственно, на 1 меньше, чем в большем числе.

Теперь рассмотрим вычитание чисел, являющихся степенями числа 2:

2³-2⁰      это 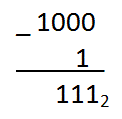 , количество нулей - 0, количество единиц - 3 (3-0)

2³-2¹      это 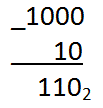, количество нулей - 1, количество единиц - 2 (3-1)

2³-2²      это ​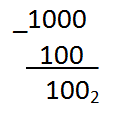, количество нулей - 2, количество единиц - 1 (3-2) и т.д.

Мы видим, что количество нулей в результате равно количеству нулей в вычитаемом числе, а количество единиц в полученном числе равно разности количества нулей в уменьшаемом и вычитаемом числах. 

Итак, сначала найдем количество единиц в разности:  2²⁰¹⁵ -2³, оно равно 2015 - 3 = 2012. Добавим одну единицу от числа 2⁴⁰²⁸, и получим результат  - 2013

 

И, в заключение, рекомендую пройти онлайн-тест В16 на сайте К.Полякова (выбрать)