Изучение мудрости возвышает и делает нас сильными и великодушными.
|
Задание № 15 (в 2020 году это было задание № 18)
Спецификация контрольных измерительных материалов единого государственного экзамена по информатике и ИКТ
| Проверяемые элементы содержания |
Уровень сложности задания |
Макс. балл за выполнение задания |
Примерное время выполнения задания |
| Знание основных понятий и законов математической логики | Повышенный | 1 | 3 |
Теория
Используя данные материалы, можно повторить необходимые теоретические вопросы.
- Материалы единой коллекции ЦОР (цифровых образовательных ресурсов):
- Материалы с сайта Фоксфорд:
- История современной логики. Информатика (Алгебра логики, теория множеств, комбинаторика) (смотреть)
- На сайте К.Ю. Полякова представлена статья по данной теме (исчерпывающая информация):
- А.П. Шестаков, Е.А. Еремин. Логические основы компьютеров // Информатика, № 12, 2010, с. 3-28.
Практика
Разберем примеры заданий из ЕГЭ прошлых лет
1. Для какого из приведённых чисел X истинно логическое условие: ¬ ((X кратно 2) → (X кратно 4))?
1) 7
2) 8
3) 10
4) 12
Преобразуем логическое выражение, обозначив простые высказывания А = (Х кратно 2), В = (Х кратно 4), ¬ ((X кратно 2) → (X кратно 4)) = ¬ (А → В) = ¬ ( ¬ А \/ В) = А /\ ¬ В.
Теперь переведем это на "понятный" язык - число Х кратно 2 и не кратно 4, это число 10.
Ответ: 3
2. На числовой прямой даны два отрезка: P = [1, 39] и Q = [23, 58].
Выберите из предложенных отрезков такой отрезок A, что логическое выражение
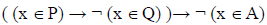
тождественно истинно, то есть принимает значение 1 при любом значении переменной х.
1) [5, 20]
2) [25, 35]
3) [40, 55]
4) [20, 40]
Введем обозначения: Р =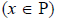 
, Q = 
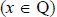, A =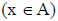 
. Получим (Р → ¬ Q) → ¬ A = (¬ P \/ ¬ Q) → ¬ A = ¬ (¬ P \/ ¬ Q) \/ ¬ A = ( P /\ Q ) \/ ¬ A.
Теперь переведем это на "понятный" язык - пересечение областей P и Q составляет отрезок (23, 39), а всё остальное пространство числовой оси должно быть покрыто областью ¬ A для того, чтобы при любом Х заданное логическое выражение равнялось единице. Из этого следует, что область А должна быть меньше или равна пересечению областей P и Q. Из предложенных вариантов подходит [25, 35]. Более наглядно можно это увидеть на чертеже.
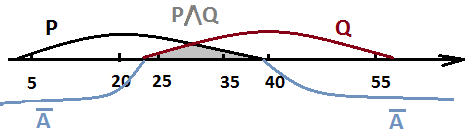
Ответ: 2
3. На числовой прямой даны два отрезка: P = [37; 60] и Q = [40; 77]. Укажите наименьшую возможную длину такого отрезка A, что формула
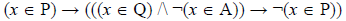
истинна при любом значении переменной х, т.е. принимает значение 1 при любом значении переменной х.
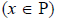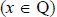Введем обозначения: Р = , Q = , A = 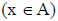. Получим P → ((Q /\ ¬ A) → ¬ P) = ¬ P \/ ((Q /\ ¬ A) → ¬ P) = ¬ P \/ ( ¬ (Q /\ ¬ A) \/ ¬ P) = ¬ P \/ ( ¬ Q \/ ¬ ¬ A \/ ¬ P) = ¬ P \/ ¬ Q \/ A \/ ¬ P = ¬ P \/ ¬ Q \/ A = ¬ (P /\ Q) \/ A
Теперь переведем это на "понятный" язык - всё пространство числовой оси должно быть покрыто областью ¬ (P /\ Q) и областью А. Область А должна быть больше или равна отрезку [40; 60], это область пересечения областей P и Q (P /\ Q), следовательно минимальный размер области равен 20 (60 - 40). Более наглядно можно это увидеть на чертеже.
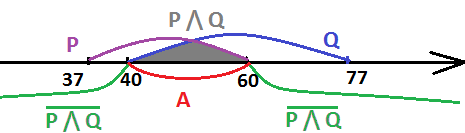
Ответ: 20
4. Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 14 & 5 = 11102 & 01012 = 01002 = 4.
Для какого наименьшего неотрицательного целого числа А формула
x & 25 ≠ 0 → (x & 17 = 0 → x & А ≠ 0) тождественно истинна (т.е. принимает значение 1 при любом неотрицательном целом значении переменной х)?
Введем обозначения: P = {x & 25 ≠ 0}, Q = {x & 17 ≠ 0}, A = { x & A ≠ 0}. Получим P → ( ¬ Q → A) = P → ( ¬ ¬ Q \/ A ) = P → ( Q \/ A ) = ¬ P \/ ( Q \/ A ) = ¬ P \/ Q \/ A
Теперь разберем, как это понимать. Для начала числа 25 и 17 представим в двоичном коде:
| разряд | 4 | 3 | 2 | 1 | 0 |
| разрядные слагаемые |
16 | 8 | 4 | 2 | 1 |
| 2510 | 1 | 1 | 0 | 0 | 1 |
| 1710 | 1 | 0 | 0 | 0 | 1 |
2510 = 110012, 1710 = 100012
Выражение ¬ P \/ Q \/ A = 1 означает, что должно быть истинным хотя бы 1 из трех высказываний: ¬ P, Q, А.
¬ P = 1 означает, что при поразрядной конъюнкции чисел 25 и х должен получиться 0. Такое может получиться только в том случае, если у числа х 4, 3 и 0 разряды равны 0 (л - любая цифра):
| разряд | 4 | 3 | 2 | 1 | 0 |
| число 2510 | 1 | 1 | 0 | 0 | 1 |
| число х | 0 | 0 | л | л | 0 |
| результат {x & 25 = 0} | 0 | 0 | л | л | 0 |
Q = 1 означает, что при поразрядной конъюнкции чисел 17 и х должна получиться 1, это может произойти, если хотя бы один из разрядов 0, 4 будет равняться 1:
| разряд | 4 | 3 | 2 | 1 | 0 |
| число 1710 | 1 | 0 | 0 | 0 | 1 |
| число х | 1 | л | л | л | 1 |
| результат {x & 17 ≠ 0} | 1 | л | л | л | 1 |
Рассмотрим вариант числа х, когда 3 разряд равен 1, а 4 и 0 равны 0 (остальные могут иметь любое значение). В этом случае ¬ P = 0 и Q = 0, это значит, что высказывание А обязательно должно быть равным 1, т.е. у числа А на месте 3 разряда должна стоять единица.
| разряд | 4 | 3 | 2 | 1 | 0 |
| число А | л | 1 | л | л | л |
| число х | 0 | 1 | л | л | 0 |
| результат { x & A ≠ 0} | 0 | 1 | л | л | 0 |
Таких чисел несколько: 01111, 01110, 01100, 01000, 01001, 01010, 01011, 01101, 11111, 11110 и т.д., а минимальное из них 10002 = 810
Ответ: 8
И, в заключение, рекомендую пройти онлайн-тест В18 на сайте К.Полякова (выбрать)
